1.引言

本文介绍了一种针对脉冲神经网络的直接监督学习方法---STBP算法：将逐层空间域（SD）和与时间相关的时域（TD）相结合，并且不需要任何其他复杂技能。在训练阶段将空间域（SD）和时间域（TD）结合在一起。首先，建立具有SNN动力学的迭代LIF模型，该模型适用于梯度下降训练。在此基础上，在误差反向传播（BP）期间同时考虑了空间维和时间维，从而明显提高了网络精度，引入近似导数来解决峰值活动的不可微问题。

2.LIF神经元模型

这里神经元模型应用的是泄漏集成并发射（LIF）是目前描述SNN中神经元动力学的最常用模型，可以通过以下方式简单地控制它：

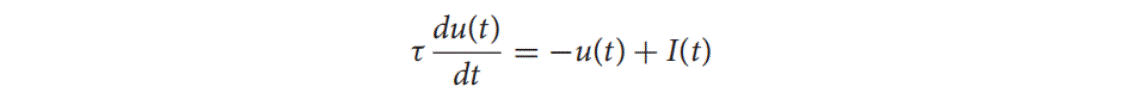
上式中的u(t)指神经元在时间t时的膜电压，τ是时间常数，I(t)表示突触前的输入，其由神经元前活动或外部注射和突触权重决定。当膜电位u(t)超过给定阈值Vth时，神经元会激发一个尖峰并将其电位重置为Ureset。然而，直接从上面式子中的LIF模型的解析解使得基于BP的离散数据流训练SNN不方便，这是因为整个网络在连续TD中呈现出复杂的动态。为了解决这个问题，首先我们用初始条件求解线性微分方程，并得到以下迭代更新规则：

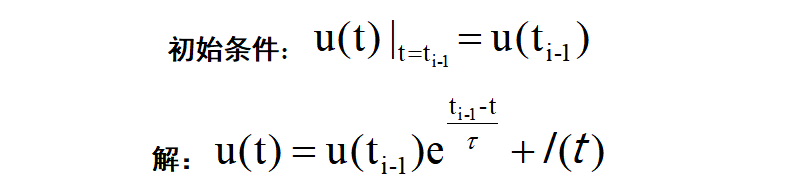
上式中u(t)神经元在时间t时的膜电压取决于前面的时间ti-1和突触前输入I(t)，膜电位呈指数衰减，直到神经元收到新的输入，一旦神经元发出尖峰，新的更新回合将开始。也就是说，神经元状态是I(t)的空间积累和的u(ti-1)时间记忆泄露决定。

我们知道，误差BP训练DNN的效率很大程度上得益于梯度下降的迭代表示，它产生了SD向后传递中逐层误差传播的链式法则，这促使我们提出了一种基于迭代LIF的SNN，其中在SD和TD中都出现了如下迭代:

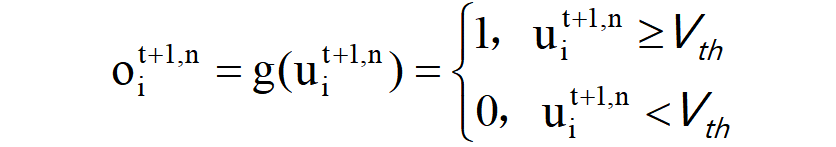
上式子主要表示：神经元最终的输出情况，在传递给下一层前需要经过一个阈值函数进行峰值处理，其中**oi(t+1,n)**代表在时间t+1时第n层中第i个神经元的输出(0或1)，g(x)函数属于一个阈值函数，当x大于等于Vth时神经元输出1(即尖峰事件)，当x小于Vth时神经元输出0(沉默)。

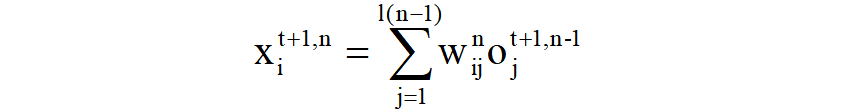
上式子主要表示：第n层的神经元接受来自第n-1层的神经元的输出，其中**xi(t+1,n)**的代表在时间t+1时第n层中第i个神经元的值，**wij(n)**代表第n层（突触前层）第j个神经元到突触后层第i个神经元的突触权重，**oj(t+1,n-1)**代表第n-1层第j个神经元的输出（0或1），它们相乘再求和算出传递过来的结果。

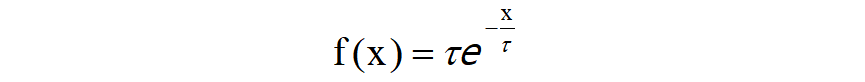
上式主要表示：衰减函数，膜电压在传递过程中随着时间会存在少部分的衰减，虽然膜电压u在整个过程中属于一个积累的过程，但是它不是只有在达到阈值时才会发生剧烈变化，根据实际的生物体神经信息传递过程，膜电压本身在传递过程中就存在少部分的衰减现象。

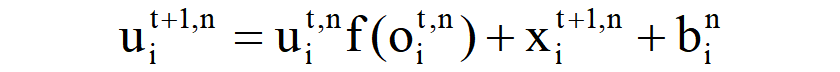
上式主要表示：膜电压u更新的过程，每个神经元在进行膜电位更新的时，其莫电压主要来自于三个部分，之前积累的膜电压(衰减了一小部分)ui(t,n)f(oi(t,n))、上一层直接传递过来的**xi(t+1,n)和一小部分偏置电压bi(n)**用于进行微调。实际上，公式也受到了LSTM模型的启发通过使用遗忘门f(x)来控制TD存储器和一个输出门g(x)来发射一个尖峰。遗忘门f(x)控制TD中潜在记忆的泄漏范围，输出门g(x)在被激活时产生一个尖峰活动。具体来说，对于一个正的时间常数，可以近似为:，这样可以将LIF模型转化为迭代版本，清晰地描述SD和TD中的递归关系，适用于后续STD中的梯度下降训练。

3.时空反传算法训练

为了介绍STBP训练框架，我们定义以下损失函数，其中给定时间窗T下所有样本的均方误差应最小化：

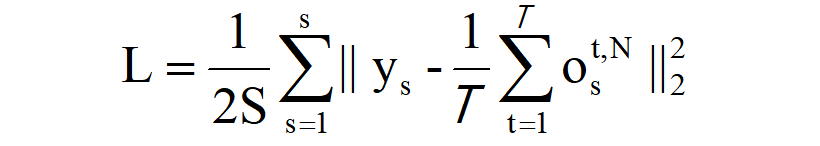
上式中ys表示训练样本的标签向量(one-hot编码)，**os(t,N)**表示在时间t时最后一层N的第s个神经元输出向量，由于它是经过时间T积累的，因此在进行均方误差计算之前，先进行均值化。最后再根据均方误差函数进行整理便可以得出上面的脉冲神经网络的损失函数的表达式。通过表达式可以看出损失函数L是关于W和b的函数，因此，对于梯度下降而言，获得损失函数相对于W和b的导数是必要的。

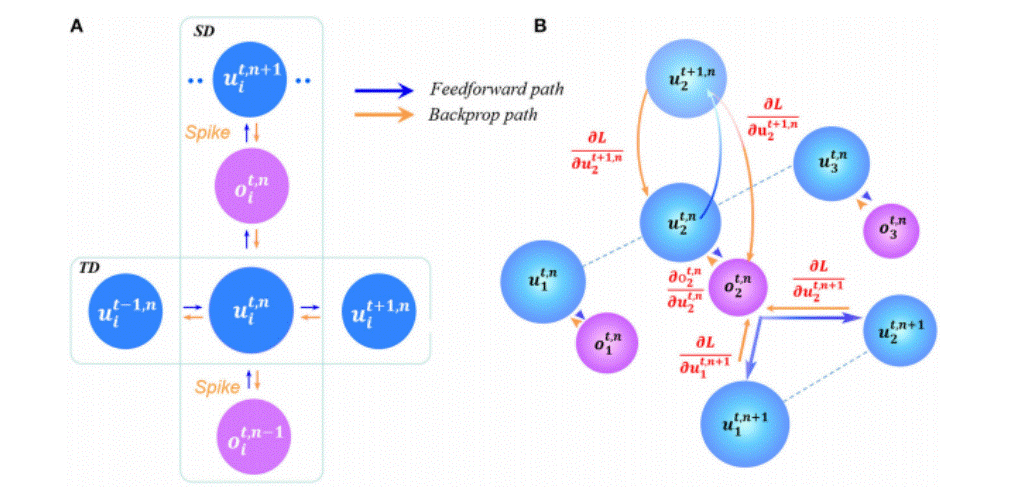
上图中主要分为两部分：SD和TD在单神经元级、网络级上的误差传播。在单神经元水平上，将传播分解为SD的垂直路径和TD的水平路径。在网络层次上，误差传播的数据流与DNN中典型的BP相似，即每个神经元从上层累积加权误差信号，并迭代更新不同层的参数;而在在TD中，神经元状态在允许链规则传播的时间维中迭代展开。

先观察图中A部分，我们把神经元ui(t,n)(在t时刻第n层第i个神经元)当作中心，分别观察水平方向TD左右：其左侧的ui(t-1,n)代表在时间t-1时刻的神经元，其右侧的ui(t+1,n)代表在时间t+1时刻的神经元，以此类推左右其实有很多个没有画出的神经元(如果设置的时间为t，则可以画出t个神经元来表示一个神经元在不同时刻的状态)，它们按照时间依次传递给下一时刻的自己(从左向右)进行前向传播，逆着时间依次沿着原路传递给之前的自己(从右向左)进行反向传播。现在，我们观察垂直方向SD上下：其下方的**oi(t,n-1)代表来自第n-1层的第i个神经元传递过来的膜电压Spike，其上方的oi(t,n)**代表传递给第n层的第i个神经元传递的膜电压Spike正向传播至第n+1层的第i个神经元。

然后，我们再观察图中B部分，其实原理类似只不过现在是侧重于网络级的传播。我们将u2(t,n)(在t时刻第n层第2个神经元)为核心,其左右分别是**u1(t,n)和u3(t,n)**两个处于同一层的神经元，其上面是u2(t+1,n)是u2(t,n)下一时刻的状态。第n层的神经元经过膜电位更新o2(t,n)将信息传递给下一层的神经元，进行前向传播。

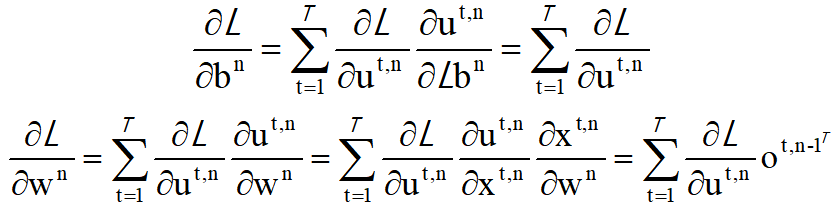
关于如何获取梯度的做法，我们在这里不再进行详细的计算推导，直接留下最终整理出的计算结果(上式)。

4.编码机制

目前较为常见的神经编码方式主要包括频率编码、时间编码、 bursting编码与群编码等。具体的脉冲在持续时间、振幅或形状上都可能有所不同，但在神经编码研究中，它们通常被视为相同的定型事件。我们本次采样编码的思路：在输入端，将实值图像转换为脉冲序列，其发射率与像素强度成正比。脉冲抽样是概率性的（例：伯努利分布、泊松分布），在输出端，它在给定的时间窗内计算最后一层每个神经元的放电速率，以确定网络输出。

脉冲神经网络的第一层输入尖峰序列，这要求我们将静态数据集中的样本转换为尖峰事件。为此，我们使用了从原始像素强度到尖峰速率的伯努利采样转换。具体地，通过使用独立且均匀分布的伯努利采样，在每个时间步长处将每个归一化像素概率性地转换为尖峰事件“1”，生成尖峰事件的概率与入口的标准化值成正比。例如：如果像素强度为0.8，则它可以在每个时间步长生成尖峰事件的概率为0.8，而保持沉默的概率为0.2，然后，某个时间窗口内的峰值事件形成峰值序列。

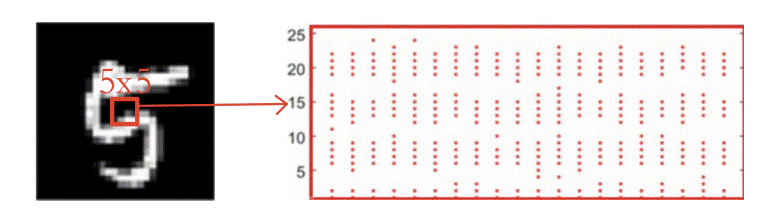
如上图所示，我们选取手写数字一张图片中5x5的一小部分展开进行可视化观察，发现经过编码后输入到模型中时只存在尖峰1和0的数字，成功实现了脉冲序列转换。

5.不可微峰活动的导数近似

前面介绍了如何基于STBP获取梯度信息，但是尚未解决每个峰值时间的不可微分问题。实际上，STBP训练需要输出门g(u)的导数，从理论上讲，g(u)是δ(u)的不可微Dirac函数，这极大地挑战了SNN的有效学习。g(u)在各处都具有零值，除了无穷大值(在零位置处)之外，这会导致梯度消失或爆炸问题，从而无法传播误差。现有方法之一将尖峰时刻电位的不连续点视为噪声，并声称它对模型的鲁棒性有益，但它没有直接解决非噪声的问题。峰值活动的可区分性。为此，我们引入了四个曲线来近似表示尖峰活动的导数：

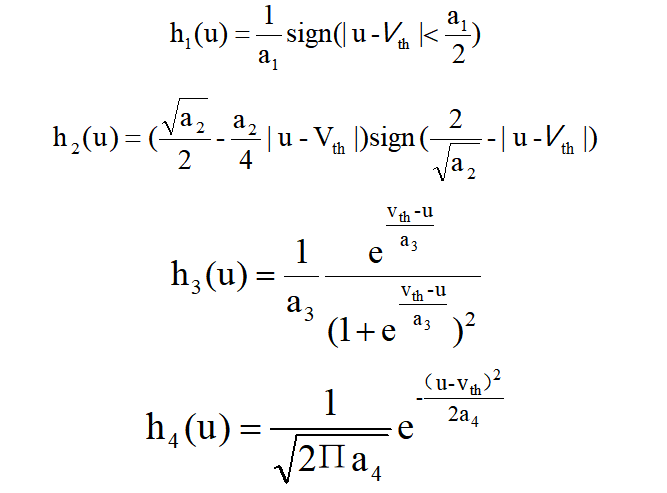
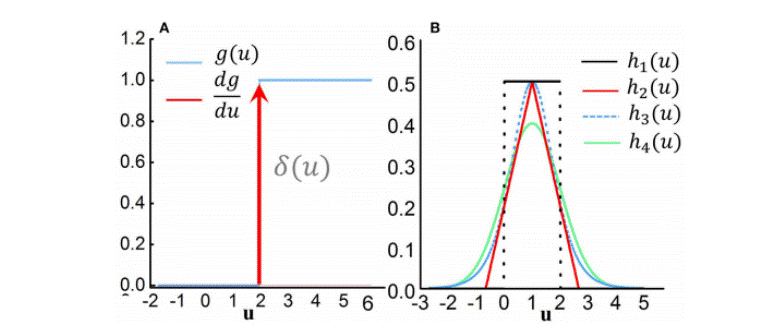
其中ai(i=1,2,3,4)决定了曲线的陡度，即峰值宽度。事实上，h1,h2,h3,h4分别是矩形函数、多项式函数、s型函数和高斯累积分布函数的导数。为了与狄拉克函数δ(u)一致，我们引入系数ai来保证每个函数的积分为1。显然，可以证明，上述候选项均满足，由此得到下面的式子。

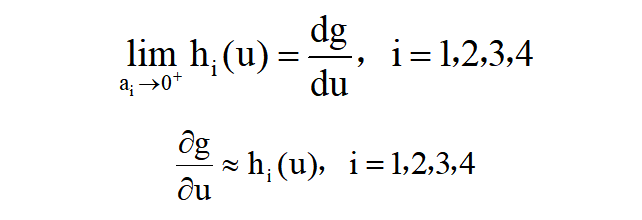
6.参数初始化

参数（例：权重、阈值等等）的初始化对于稳定整个网络的触发活动至关重要。我们应该同时确保突触前刺激的及时响应，但要避免过多的尖峰降低神经元的选择性。众所周知，预峰值和 权重的乘加运算以及阈值比较是前向传递中的两个关键计算步骤。这表明权重和阈值之间的相对大小决定了参数初始化的有效性。在本文中，为简化起见，我们将阈值固定为每个神经元中的常数，并且仅调整权重以控制活动平衡。首先，我们通过从标准均匀分布式中采样来初始化所有权重参数：

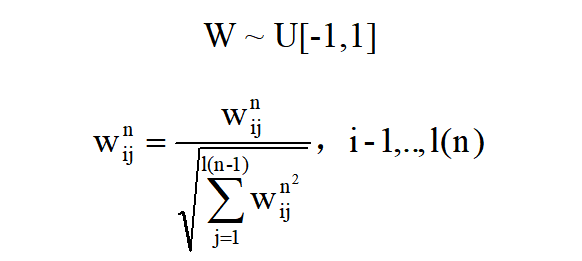
我们通过上面第二个式子的方式归一化这些参数。此外，Adam是一种常用的加速梯度下降收敛速度的优化方法，当根据参数的梯度更新参数W和b时，我们使用ANN中常用的Adam优化器。实际上，它并不影响梯度获取过程，只是用于参数更新。此外，在我们的所有模拟工作中，任何复杂的技能，不再需要，如：误差归一化、权值/阈值正则化、定量-比例复位机制等。

7.模型结构及性能

我们构建了2个浅层的脉冲神经网络应用于MNIST与CIFAR10，其网络的结构如下：

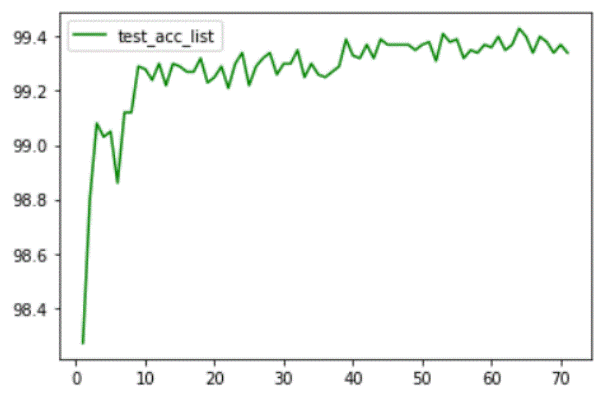
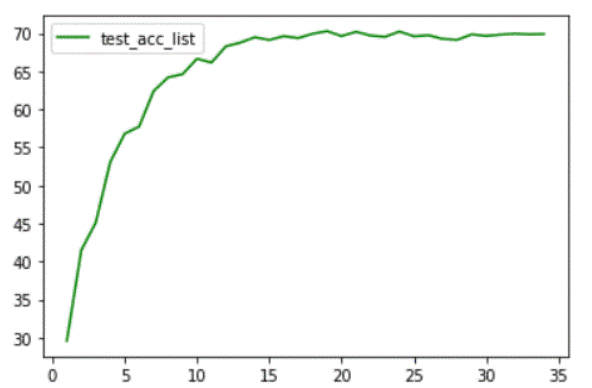
SNN_STBP_MNIST和SNN_STBP_CIFAR10两个网络模型的性能图像分别如下图所示。对于SNN_STBP_MNIST模型很快便能达到很高的正确率，随后稳定在99.4%左右。对于SNN_STBP_CIFAR10模型，刚开始损失比较严重，随着训练次数的增加，模型正确率稳定于70%左右便不再升高。

8.存在的问题

目前的难度主要涉及两个方面：首先，由于复杂的动力学和不可分的尖峰活动，在此阶段直接实施BP算法来训练SNN具有挑战性。其次，尽管在专门的神经形态芯片上实现SNN效率很高，但是在计算机软件上模拟SNN的复杂动力学行为却非常困难且耗时（与相同结构的ANN相比，运行时间是其十倍甚至一百倍）。因此，加速基于CPU/GPU或神经形态基质的大规模SNN的有监督训练在将来也值得研究。

资源链接

• LYS的Github中基于STBP训练的SNN源码
• Probabilistic Firing of Neurons
• 查看GPU信息
• 单机多卡训练：pytorch如何使用多块GPU
• 单机多卡训练：pytorch多GPU训练总结
• 单机多卡训练：Pytorch多GPU计算之torch.nn.DataParallel()
• 报错：Expected object of device type cuda but got device type cpu for argument #1
• 报错：RuntimeError: Input type (torch.cuda.FloatTensor) and weight type (torch.FloatTensor)

参考文献

[1] Wu Y, Deng L, Li G, et al. Direct training for spiking neural networks: Faster, larger, better[C]. Proceedings of the AAAI Conference on Artificial Intelligence:volume 33. 2019: 1311-1318.

[2] Wu, Y., and He, K. 2018. Group normalization. arXiv preprint arXiv:1803.08494.

[3] Wu, Y.; Deng, L.; Li, G.; Zhu, J.; and Shi, L. 2018. Spatio temporal backpropagation for training high-performance spiking neural networks. Frontiers in Neuroscience 12.

[4] Lee, C., Sarwar, S. S., and Roy, K. (2019a). Enabling spike-based backpropagation in state-of-the-art deep neural network architectures. arXiv [Preprint].arXiv:1903.06379.

[5] Lee, C., Srinivasan, G., Panda, P., and Roy, K. (2019b). Deep spiking convolutional neural network trained with unsupervised spike-timing-dependent plasticity. IEEE Trans. Cogn. Dev. Syst. 11, 384–394. doi: 10.1109/TCDS.2018.28 33071