自然语言处理涉及多个子领域，但是它们的根本任务就是让计算机理解我们的语言，在深度学习出现之前也存在一些传统方法，当然要想理解深度学习如何处理自然语言的任务，背后的原理是什么，必须先理解方法。

1.什么是自然语言处理

我们平时使用的语言，如日语、英语，称为自然语言(Natural Language)。而自然语言处理(Natural Language Processing，NLP)就是处理自然语言的科学：简单的说就是一种能够让计算机理解人类语言的技术，进而完成对我们有帮助的任务。

另外，提到计算机可以理解的语言，我们可能会想到编程语言或标记语言等等。但是，编程语言是一种机械的缺乏活力的语言，它是一种“硬语言”，而英语或日语均属于“软语言”----意思和形式灵活多变。另外，自然语言的“软”还体现在，新的词语或新的含义会随着时代的发展不断出现。事实上，我们可以看到很多这样的应用：搜索引擎、机器翻译、问答系统、自动文本摘要、情感分析等等。

我们的语言是由文字构成的，单词是最小的单位。因此，要想让计算机理解自然语言的前提就是让其理解每个单词的含义。我们主要有3种方法实现：

基于同义词词典的方法
基于计数的方法
基于推理的方法（word2vec）

2.同义词词典

同义词词典：具有相同含义的单词或含义类似的单词（近义词）被归为同一组中。比如，使用同义词词典表示一下car相关的单词如下图所示：

另外，在自然语言处理中应用的同义词词典有时会定义单词之间更细的关系，比如：“上位---下位”关系，“整体---部分”关系（如下图所示），利用这种“单词网络”可以教会计算机单词之间的相关性。

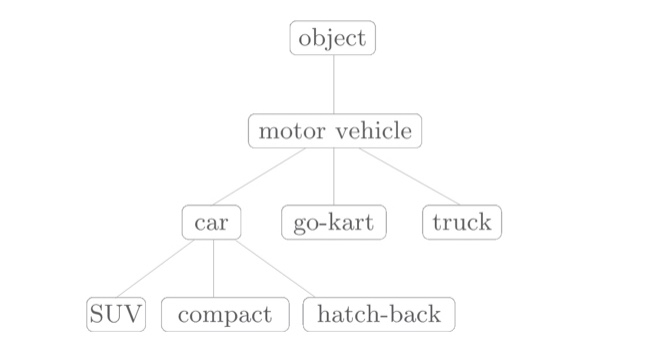
2.1 WordNet

在自然语言处理领域中，最著名的同义词词典是“WordNet”---普林斯顿大学于1985年开始开发的同义词词典。使用WordNet可以获得单词的近义词，或者使用单词网络(计算单词之间的相似度)。安装WordNet可以尝试安装NLTK模块，利用pip进行安装：

$ pip install nltk

2.2 同义词词典的问题

WordNet等同义词词典中对大量单词定义了同义词和层级结构关系等，利用这些知识，可以（间接地）让计算机理解单词含义。但是，人工标记也存在一些较大的缺陷：

难以顺应时代变化：随着时间的推移，新词不断出现，而那些落满尘埃的旧词不知哪天就会被遗忘。另外，语言的含义也会随着时间的推移而变化，人力成本高
巨大的人力成本：以英文为例，据说现有的英文单词总数超过 1000 万个。在极端情况下，还需要对如此大规模的单词进行单词之间的关联。顺便提一下，WordNet 中收录了超过 20 万个的单词。
无法表示单词的微妙差异：同义词词典中将含义相近的单词作为近义词分到一组。但实际上，即使是含义相近的单词，也有细微的差别，而这种细微的差别在同义词词典中是无法表示出来的。

因此，为了避免这些问题，人们发展出了：基于计数的方法，利用神经网络的基于推理的方法。这两种方法可以从海量的文本数据中自动提取单词含义，将我们从人工关联单词的辛苦劳动中解放出来。

3.基于计数的方法

从基于计数的方法开始，我们将使用语料库(corpus)---大量的文本数据,用于自然语言处理研究和应用的文本数据，其中的文章都是由人写出来的。换句话说，语料库中包含了大量的关于自然语言的实践知识，即文章的写作方法、单词的选择方法和单词含义等。基于计数的方法的目标就是从这些富有实践知识的语料库中，自动且高效地提取本质。

3.1 语料库的预处理

自然语言处理领域存在各种各样的语料库，如：Wikipedia和Google-News等等...现在，我们对一个非常小的文本数据（语料库）进行预处理。这里所说的预处理是指：

将文本分割成单词
单词列表转化为单词ID列表

这里，我们简化语料库(本来文本应该包含成千上万个连续的句子)，但是为了方便这里仅采用一句话的文本数据进行实验：首先，将文本中的字母全部转换成小写，这样可以将句子的开头的单词也作为常规单词处理；然后，将空格作为分隔符，因此要将句子最后的标点“.”更换成“ .”多插入一个空格，再进行分词：

>>> text = 'You say goodbye and I say hello.'
>>> text = text.lower()
>>> text = text.replace('.', ' .')
>>> text
you say goodbye and I say hello .
>>> words = text.split(' ')
>>> words
['you', 'say', 'goodbye', 'and', 'i', 'say', 'hello', '.']

虽然分词后文本更容易处理了，但是直接以文本形式操作单词而不是数字形式，并不是特别方便。因此。我们将对单词列表进一步操作：转换成单词ID列表

>>> word_to_id = {}
>>> id_to_word = {}
>>> for word in  words:
		    if word not in word_to_id:
				  new_id = len(word_to_id)
				  word_to_id[word] =  new_id
				  id_to_word[new_id] = word

>>> word_to_id
{'and': 3, 'i': 4, '.': 6, 'say': 1, 'goodbye': 2, 'you': 0, 'hello': 5}
>>> id_to_word
{0: 'you', 1: 'say', 2: 'goodbye', 3: 'and', 4: 'i', 5: 'hello', 6: '.'}

使用这些词典，可以根据单词检索单词ID，或者反过来根据单词 ID 检索单词：

>>> word_to_id['and']
3
>>> id_to_word[3]
and

最后，我们将单词列表转化为单词ID列表，并将其转化为Numpy数组：

>>> import numpy as np
>>> corpus =  [word_to_id[w] for  w in words]
>>> corpus
array([0, 1, 2, 3, 4, 1, 5, 6])

到此，我们就实现了语料库的预处理工作，我们上面的代码整合到一个函数中：

def preprocess(text):
    text = text.lower()
    text = text.replace('.', ' .')
    words = text.split(' ')

    word_to_id = {}
    id_to_word = {}
    for word in words:
        if word not in word_to_id:
            new_id = len(word_to_id)
            word_to_id[word] = new_id
            id_to_word[new_id] = word

    corpus = np.array([word_to_id[w] for w in words])

    return corpus, word_to_id, id_to_word

3.2 单词的分布式表示

我们能不能将类似于颜色RGB表示方法运用到单词上呢？在单词领域构建紧凑合理的向量表示，在自然语言处理领域，这称为分布式表示。单词的分布式表示将单词表示为固定长度的向量。这种向量的特征在于它是用密集向量表示的。密集向量：向量的各个元素（大多数）是由非 0 实数表示的。例如，三维分布式表示是 [0.21,-0.45,0.83]。

3.3 分布式假设

“某个单词的含义由它周围的单词形成”，称为分布式假设。分布式假设所表达的理念非常简单，单词本身没有含义，单词含义由它所在的上下文(语境)形成。含义相同的单词经常出现在相同的语境中，比如“I drink beer.”“We drink wine.”，drink 的附近常有饮料出现。另外，从“I guzzle beer.”“We guzzle wine.”可知，guzzle 和 drink 所在的语境相似。进而我们可以推测出，guzzle 和 drink 是近义词（guzzle ：“大口喝”）。

我们将某个词的上下文的大小(即周围的单词有多少个)称为窗口大小(window size)。例如：窗口大小为 1，上下文包含左右各 1 个单词；窗口大小为 2，上下文包含左右各 2 个单词，以此类推...我们将左右两边相同数量的单词作为上下文。但是，根据具体情况，也可以仅将左边的单词或者右边的单词作为上下文。此外，也可以使用考虑了句子分隔符的上下文。简单起见，我们现在仅处理不考虑句子分隔符、左右单词数量相同的上下文。

3.4 共现矩阵

下面，我们来考虑如何基于分布式假设使用向量表示单词，最直截了当的实现方法是对周围单词的数量进行计数。具体来说，在关注某个单词的情况下，对它的周围出现了多少次什么单词进行计数，然后再汇总。这里，我们将这种做法称为“基于计数的方法”，在有的文献中也称为“基于统计的方法”。

这里我们使用之前的语料库和preprocess()函数，再次进行预处理：

>>>import sys
>>>sys.path.append('..')
>>>import numpy as np
>>>from Deep_Learning_up.common.util import preprocess

>>>text = 'You say goodbye and I say hello.'
>>>corpus, word_to_id, id_to_word = preprocess(text)
>>>print(corpus)
[0 1 2 3 4 1 5 6]
>>>print(word_to_id)
{'and': 3, 'i': 4, '.': 6, 'say': 1, 'goodbye': 2, 'you': 0, 'hello': 5}
>>>print(id_to_word)
{0: 'you', 1: 'say', 2: 'goodbye', 3: 'and', 4: 'i', 5: 'hello', 6: '.'}

下面，我们计算每个单词的上下文所包含的单词的频数。在这个例子中，我们将窗口大小设为 1，从单词 ID 为 0 的 you 开始。从图中可以清楚地看到，单词 you 的上下文仅有 say 这个单词。用表格表示的话，如下图表示：

上图中的表表示的是作为单词 you 的上下文共现的单词的频数。同时，这也意味着可以用向量 [0, 1, 0, 0, 0, 0, 0] 表示单词 you。接着对单词 ID 为 1 的 say 进行同样的处理，结果如下图所示：

从上面的结果可知，单词 say 可以表示为向量 [1, 0, 1, 0, 1, 1, 0]。对所有的 7 个单词进行上述操作，会得到下图所示的结果：

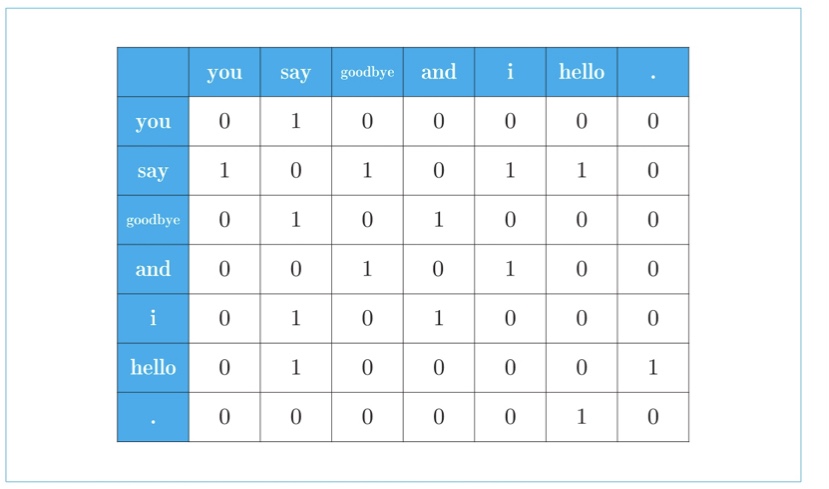
上图是汇总了所有单词的共现单词的表格。这个表格的各行对应相应单词的向量。因为图中的表格呈矩阵状，所以称为共现矩阵（co-occurence matrix）。下面是具体的代码实现(整个过程写在函数中)：

def create_co_matrix(corpus, vocab_size, window_size=1):
    '''生成共现矩阵
    :param corpus: 语料库（单词ID列表）
    :param vocab_size:词汇个数
    :param window_size:窗口大小（当窗口大小为1时，左右各1个单词为上下文）
    :return: 共现矩阵
    '''
    corpus_size = len(corpus)
    co_matrix = np.zeros((vocab_size, vocab_size), dtype=np.int32)

    for idx, word_id in enumerate(corpus):
        for i in range(1, window_size + 1):
            left_idx = idx - i
            right_idx = idx + i

            if left_idx >= 0:
                left_word_id = corpus[left_idx]
                co_matrix[word_id, left_word_id] += 1

            if right_idx < corpus_size:
                right_word_id = corpus[right_idx]
                co_matrix[word_id, right_word_id] += 1

    return co_matrix

调用函数进行测试，发现与预想的结果一样：

>>>corpus, word_to_id, id_to_word = preprocess(text)
>>>vocab_size = len(word_to_id)
>>>C = create_co_matrix(corpus, vocab_size)
>>>print(C)
[[0 1 0 0 0 0 0]
 [1 0 1 0 1 1 0]
 [0 1 0 1 0 0 0]
 [0 0 1 0 1 0 0]
 [0 1 0 1 0 0 0]
 [0 1 0 0 0 0 1]
 [0 0 0 0 0 1 0]]

3.5 向量的相似度

测量向量间的相似度有很多方法，其中具有代表性的方法：向量内积或欧式距离等。虽然除此之外还有很多方法，但是在测量单词的向量表示的相似度方面，余弦相似度（cosine similarity）是很常用的，具体公式如下：

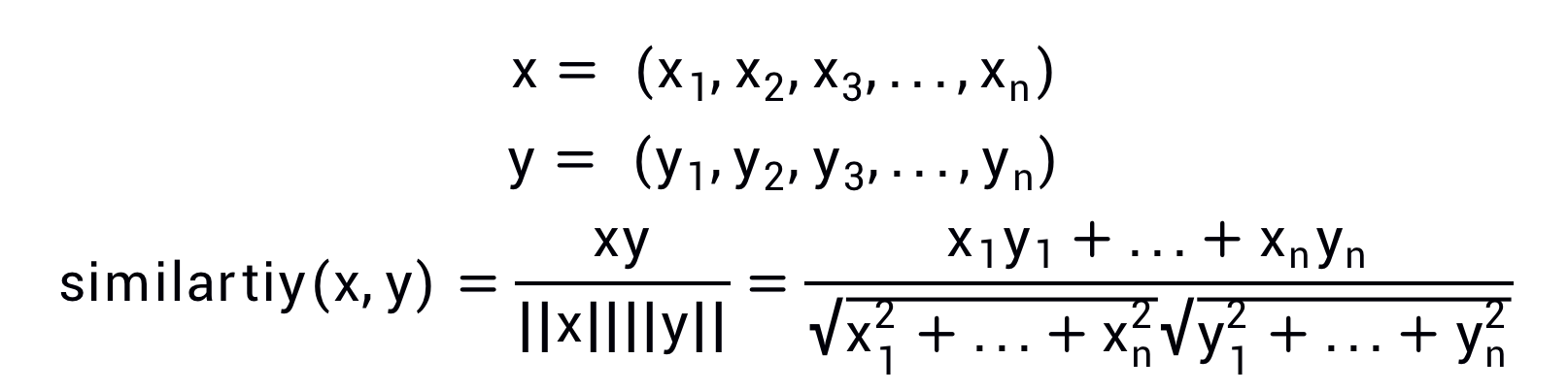
屏幕快照 2020-12-23 15.27.22.png

这里，我们假定参数x和y是NumPy数组。首先对向量进行正规化，然后求两个向量的内积。这里余弦相似度的实现虽然完成了，但是还有一个问题。那就是当零向量(元素全部为 0 的向量)被赋值给参数时，会出现“除数为 0”(zero division)的错误。解决此类问题的一个常用方法是，在执行除法时加上一个微小值。这里，通过参数指定一个微小值 eps(eps 是 epsilon 的缩写)，并默认 eps=1e-8(=0.000 000 01)

def cos_similarity(x, y, eps=1e-8):
    nx = x / (np.sqrt(np.sum(x ** 2)) + eps)
    ny = y / (np.sqrt(np.sum(y ** 2)) + eps)
    return np.dot(nx, ny)

这里我们用了1e-8作为微小值，在这么小的值的情况下，根据浮点数的舍入误差，这个微小值会被其他值“吸收”掉。在上面的实现中，因为这个微小值会被向量的范数“吸收”掉，所以在绝大多数情况下，加上 eps 不会对最终的计算结果造成影响。而当向量的范数为 0 时，这个微小值可以防止“除数为 0”的错误。下面利用这个函数，求得单词you与i之间的相似度：

>>> text = 'You say goodbye and I say hello.'
>>> corpus, word_to_id, id_to_word = preprocess(text)
>>> vocab_size = len(word_to_id)
>>> C = create_co_matrix(corpus, vocab_size)
>>> c0 = C[word_to_id['you']]  # you的单词向量
>>> c1 = C[word_to_id['i']]    # i的单词向量
>>> print(cos_similarity(c0, c1))
0.7071067691154799

从上面的结果可知，you和i的余弦相似度是 0.70(余弦相似度的取值范围：-1~1)。

3.6 相似的单词排列

编写一个函数：查询与传入的单词相似度最高的前几位。

def most_similar(query, word_to_id, id_to_word, word_matrix, top=5):
    '''相似单词的查找
    :param query: 查询词
    :param word_to_id: 从单词到单词ID的字典
    :param id_to_word: 从单词ID到单词的字典
    :param word_matrix: 汇总了单词向量的矩阵，假定保存了与各行对应的单词向量
    :param top: 显示到前几位
    '''
	# 1.取出查询词的向量
    if query not in word_to_id:
        print('%s is not found' % query)
        return
    print('\n[query] ' + query)
    query_id = word_to_id[query]
    query_vec = word_matrix[query_id]
	
	# 2.计算余弦相似度
    vocab_size = len(id_to_word)
    similarity = np.zeros(vocab_size)
    for i in range(vocab_size):
        similarity[i] = cos_similarity(word_matrix[i], query_vec)
	
	# 3.基于余弦相似度，按照降序输出
    count = 0
    for i in (-1 * similarity).argsort(): # argsort()：返回数组各个元素对应原数组的索引
        if id_to_word[i] == query:
            continue
        print(' %s: %s' % (id_to_word[i], similarity[i]))
        count += 1
        if count >= top:
            return

调用函数进行测试，显示出前5个相关度最高的单词：

>>> text = 'You say goodbye and I say hello.'
>>> corpus, word_to_id, id_to_word = preprocess(text)
>>> vocab_size = len(word_to_id)
>>> C = create_co_matrix(corpus, vocab_size)
>>> most_similar('you', word_to_id, id_to_word, C, top=5)
[query] you
goodbye: 0.7071067691154799
i: 0.7071067691154799
hello: 0.7071067691154799
say: 0.0
and: 0.0

观察结果可知，和you最接近的单词有：goodbye、i和hello。因为i和you都是人称代词，所以二者相似可以理解。但是，goodbye和hello的余弦相似度也很高，这和我们的感觉存在很大的差异。一个可能的原因是：这里的语料库太小了。

3.7 点互信息

共现矩阵的元素：两个单词同时出现的次数。但是，这种方法存在很大的问题：如何应对高频词汇？比如，我们来考虑某个语料库中the和car共现的情况。在这种情况下，我们会看到很多“...the car...”这样的短语。因此，它们的共现次数将会很大。另外，car和drive也明显有很强的相关性。但是，如果只看单词的出现次数，那么与drive相比，the和car的相关性更强。这意味着，仅仅因为 the 是个常用词，它就被认为与car有很强的相关性。为了解决这一问题，可以使用点互信息(PMI)这一指标：对于随机变量x和y，它们的PMI定义如下：

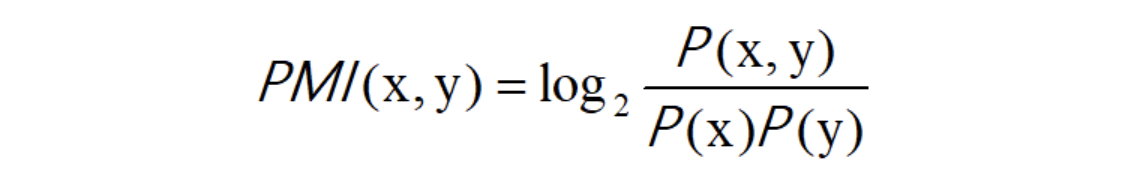
其中，P(x)表示x发生的概率，P(y)表示y发生的概率，P(x,y)表示x和y同时发生的概率。PMI的值越高，表明相关性越强。现在，我们使用共现矩阵（C：单词共现的次数,N：词库单词总数）来重新整理表达式：

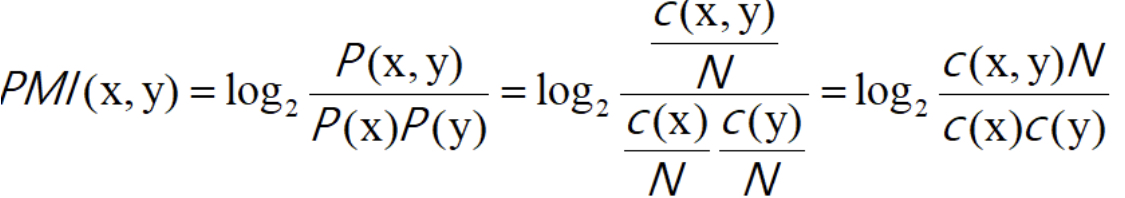
举个例子：词库单词总数N=10000，the出现100次，car出现20次，drive出现10次，the和car共现10次，car和drive共现5次，求它们对应的PMI值：

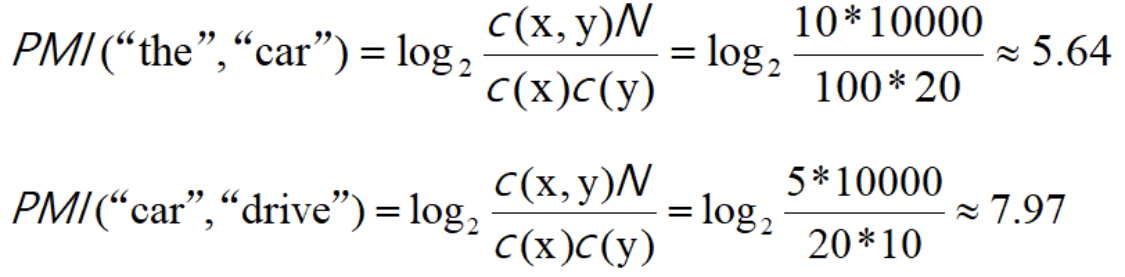
由此可见，在使用PMI的情况下，与the相比，drive和car具有更强的相关性。这是我们想要的结果。之所以出现这个结果，是因为我们考虑了单词单独出现的次数。在这个例子中，因为 the 本身出现得多，所以 PMI 的得分被拉低了。但是PMI也有一个问题：那就是当两个单词的共现次数为0时，PMI=-∞。为了解决这个问题，实践上我们会使用下述正点互信息（PPMI）：

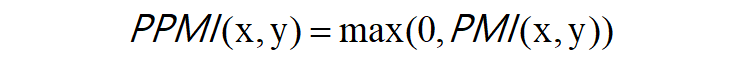
下面，我们通过函数实现PPMI的功能：

def ppmi(C, verbose=False, eps = 1e-8):
    '''生成PPMI（正的点互信息）
    :param C: 共现矩阵
    :param verbose: 是否输出进展情况
    :return:
    '''
    M = np.zeros_like(C, dtype=np.float32)
    N = np.sum(C)
    S = np.sum(C, axis=0)
    total = C.shape[0] * C.shape[1]
    cnt = 0

    for i in range(C.shape[0]):
        for j in range(C.shape[1]):
            pmi = np.log2(C[i, j] * N / (S[j]*S[i]) + eps)
            M[i, j] = max(0, pmi)

            if verbose:
                cnt += 1
                if cnt % (total//100 + 1) == 0:
                    print('%.1f%% done' % (100*cnt/total))
    return M

下面我们调用上面的函数，将共现矩阵转换成PPMI矩阵：

>>> text = 'You say goodbye and I say hello.'
>>> corpus, word_to_id, id_to_word = preprocess(text)
>>> vocab_size = len(word_to_id)
>>> C = create_co_matrix(corpus, vocab_size)
>>> W = ppmi(C)
>>> np.set_printoptions(precision=3)
>>> print(C)
[[0 1 0 0 0 0 0]
 [1 0 1 0 1 1 0]
 [0 1 0 1 0 0 0]
 [0 0 1 0 1 0 0]
 [0 1 0 1 0 0 0]
 [0 1 0 0 0 0 1]
 [0 0 0 0 0 1 0]]
>>> print(W)
[[0.    1.807 0.    0.    0.    0.    0.   ]
 [1.807 0.    0.807 0.    0.807 0.807 0.   ]
 [0.    0.807 0.    1.807 0.    0.    0.   ]
 [0.    0.    1.807 0.    1.807 0.    0.   ]
 [0.    0.807 0.    1.807 0.    0.    0.   ]
 [0.    0.807 0.    0.    0.    0.    2.807]
 [0.    0.    0.    0.    0.    2.807 0.   ]]

尽管PPMI矩阵能够改善之前共现矩阵存在的高频词汇问题，但是这两种方法都存在一个共性问题：随着单词数目的增加，矩阵的维数也在增加，而其中很多元素都为0(不重要的元素)；向量容易受到噪声的影响，稳定性差。

参考书籍

《深度学习进阶---自然语言处理》：[日]斋藤康毅

《深度学习》：[美]伊恩古德费洛

自然语言处理01---单词的分布式表示