
自然语言处理02---word2vec
1.基于推理的方法和神经网络
1.1 基于计数的方法的问题
“基于计数的方法”是根据一个单词周围的单词出现的频数来表示该单词,先是获取所有单词的共现矩阵,再利用PPMI进行转换,最后进行降维以获取密集向量(单词的分布式表示)。然而,现实生活中的语料库处理的单词数量非常庞大,面对如此庞大的矩阵,虽然降维可以在一定程度上提高处理速度,但是还是会消耗大量计算资源和时间。
1.2 基于推理的方法
“基于推理的方法”的核心在于推理,当给出周围的单词(上下文)时,预测中间可能出现什么样的单词,如下图所示:
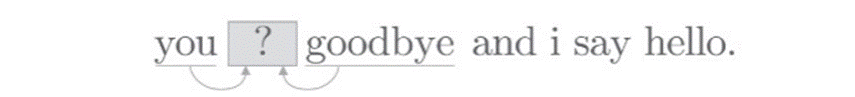
整个推理过程是需要模型事先进行学习后,才能准确预测的,通过让神经网络反复求解这些推理问题,让其学习到单词出现的规律,每次遇到上下文时,经过模型的计算筛选出可能出现的单词,最后选取概率最大的选项:
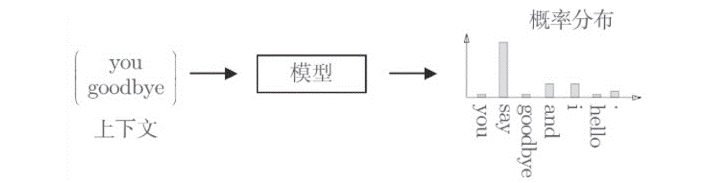
另外,作为模型学习的产物,我们可以从其内部得到单词的分布式表示(基于“分布式假设”)。
1.3 如何向神经网络输入单词
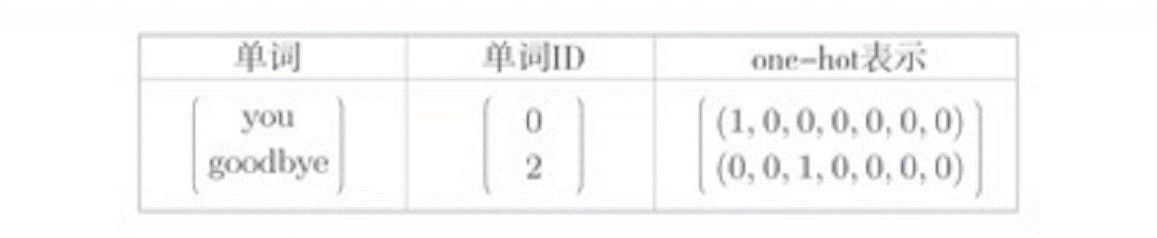
神经网络无法直接处理像单词这样的文本数据,因此需要先将单词转换成固定长度的向量,如:one-hot。我们用之前一句话的语料库来举例,如下图所示,像这样,将单词转化为固定长度的向量,神经网络的输入层的神经元个数就能固定下来。
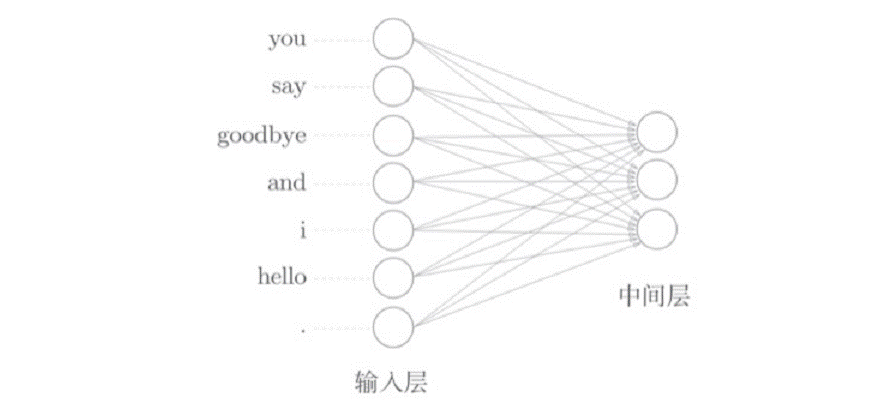
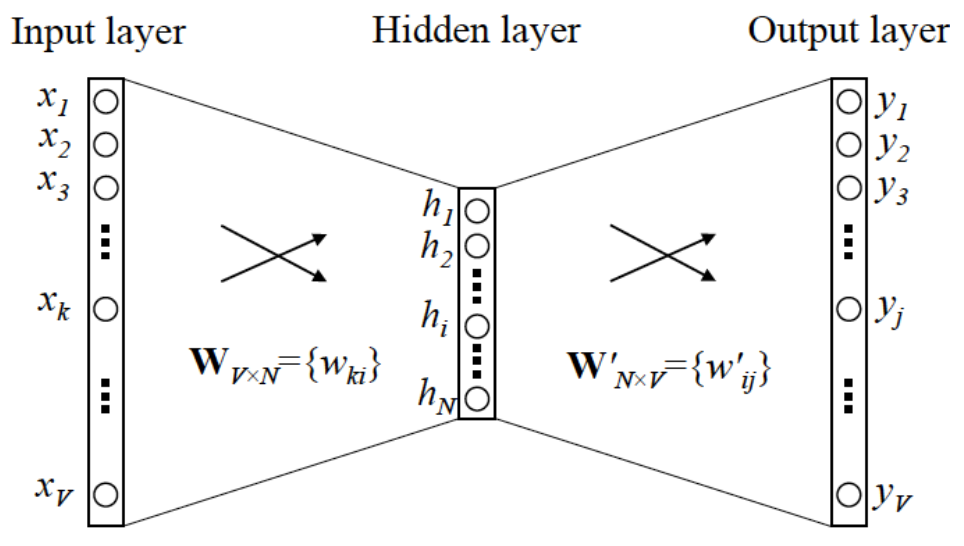
根据上面的网络结构,利用代码实现:
import numpy as np
# 创建MatMul层
class MatMul:
def __init__(self, W):
self.params = [W]
self.grads = [np.zeros_like(W)]
self.x = None
def forward(self, x):
W, = self.params
out = np.dot(x, W)
self.x = x
return out
def backward(self, dout):
W, = self.params
dx = np.dot(dout, W.T)
dW = np.dot(self.x.T, dout)
self.grads[0][...] = dW
return dx
# 模拟神经网络:输入层传入下一层的过程
c = np.array([[1,0,0,0,0,0,0]])
w = np.random.randn(7,3)
layer = MatMul(w)
h = layer.forward(c)
print(w)
print(h)
[[ 0.02208048 -1.08311824 1.14424634]
[-0.05840212 0.50722317 2.40452571]
[ 1.6279669 0.16726447 2.31558154]
[-0.34342874 -0.51914522 1.366774 ]
[ 1.61647284 -1.20494767 0.53249363]
[-1.509456 -0.48079671 1.25956899]
[-0.76804262 0.17895199 1.55890368]]
[[ 0.02208048 -1.08311824 1.14424634]]
此时,c与w进行矩阵相乘等价于“提取”权重中对应的行向量(实际上,这样的做法并不是很有效),如下图所示:
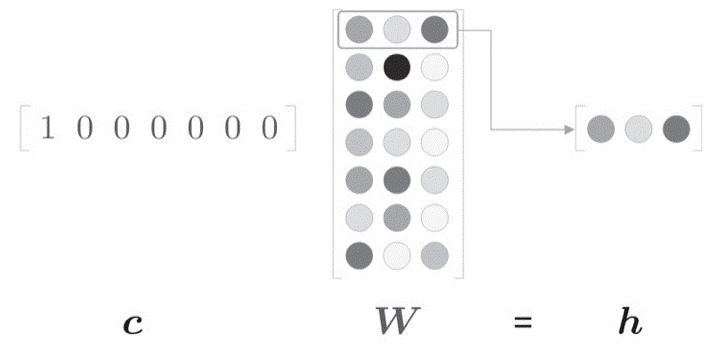
2.简单的word2vec
Word2vec是一群用来产生词向量的相关模型(浅而双层的神经网络),但它的最终目的并不是不是要把模型训练得多么完美,而是关心模型训练完后的副产物—-—“模型参数”(神经网络的权重),并将这些参数,作为输入x的某种向量化的表示,这个向量便叫做“词向量”。其中,存在两个常见的模型:
- Skip-gram 模型:如果是用一个词语作为输入,来预测它周围的上下文
- CBOW 模型:如果是用一个词语的上下文作为输入,来预测这个词语本身
2.1 CBOW模型的推理
CBOW模型的“目标词”指中间的单词,“输入”指上下文。现在,我们假设上下文的单词为1(目标词的左右各一个单词),绘画出下图所示的网络结构,它有两个输入层,经过中间层到达输出层:
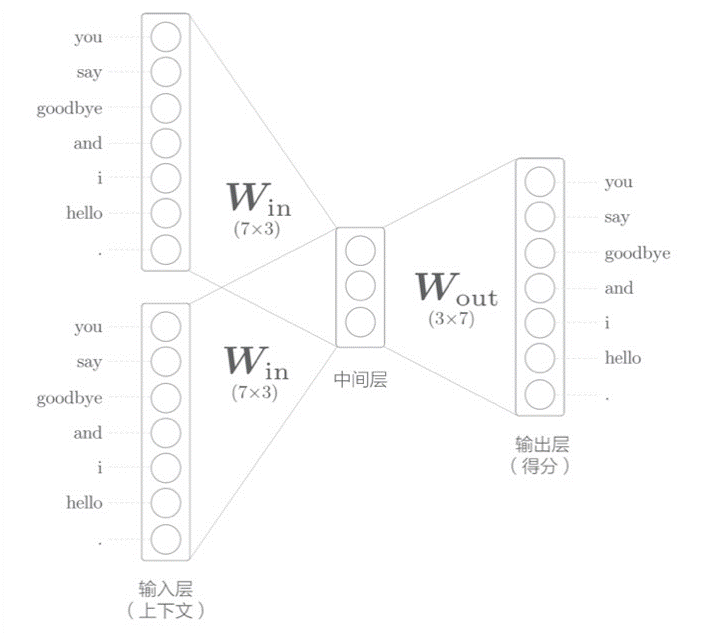
对于输入层存在两层的情况下,我们可以采用取平均值的方案来处理,中间层的神经元是各个输入层全连接层变换后得到的值的“平均”:设第一个输入层转化是h1,第二个输入层转换是h2,则中间层的神经元是(h1+h2)/2。最后的输出层有7个神经元,这些神经元对应着各个单词的得分(分值越大,出现的可能性越大,也可以在此应用Softmax函数获取对应的概率)。实际上,输入层到中间层的变化有全连接层(权重W的矩阵)就是我们需要的单词分布式表示,每一行保存着各个单词的表示,通过不断学习,不断更新。
中间层的神经元数量比输入层少:中间层需要将预测单词所需的信息压缩保存,从而产生密集的向量表示。中间层中人们无法解读的代码相当于“编码”,而从中间层的信息获得期望结果的过程相当于“解码”。
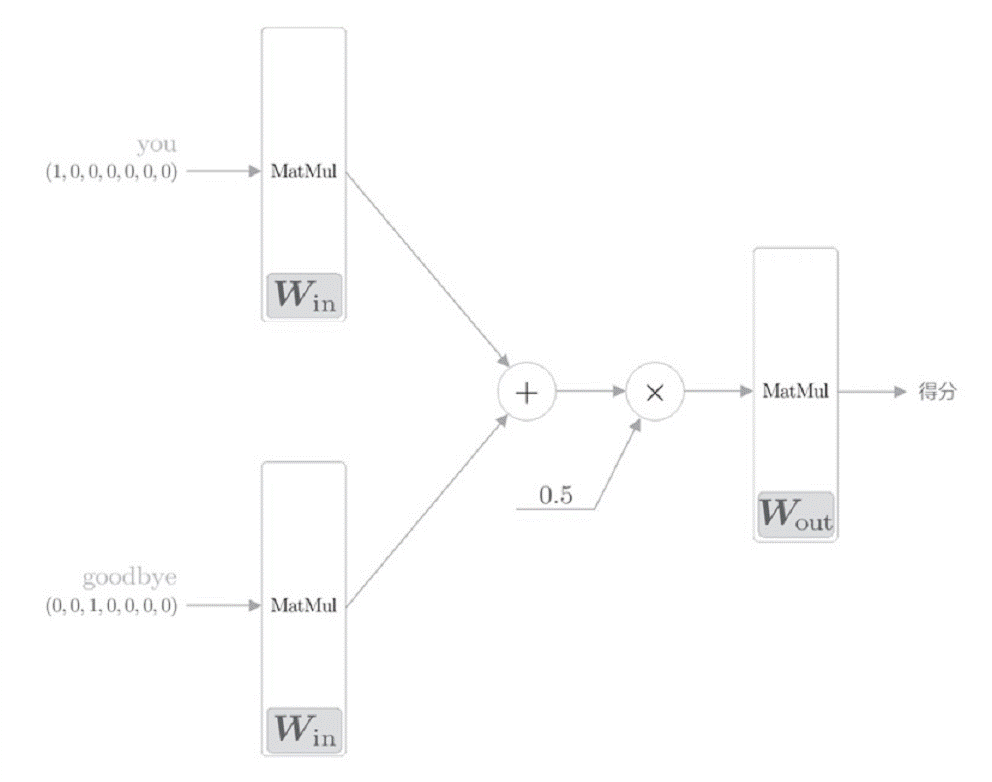
我们将之前的网络模型图画的再详细一些,并利用代码实现整个过程:
import numpy as np
# 上下文:you和goodbye
c0 = np.array([[1, 0, 0, 0, 0, 0, 0]])
c1 = np.array([[0, 0, 1, 0, 0, 0, 0]])
# 初始化权重
W_in = np.random.randn(7, 3)
W_out = np.random.randn(3, 7)
# 生成层
in_layer0 = MatMul(W_in)
in_layer1 = MatMul(W_in)
out_layer = MatMul(W_out)
# 正向传播
h0 = in_layer0.forward(c0)
h1 = in_layer1.forward(c1)
h = 0.5 * (h0 + h1)
s = out_layer.forward(h)
# 查看输出层:各单词的得分
print(s)
[[-1.50448453 1.14237664 -0.79033086 2.00505117 0.21321036 0.43664336 2.21589136]]
2.2 CBOW模型的学习
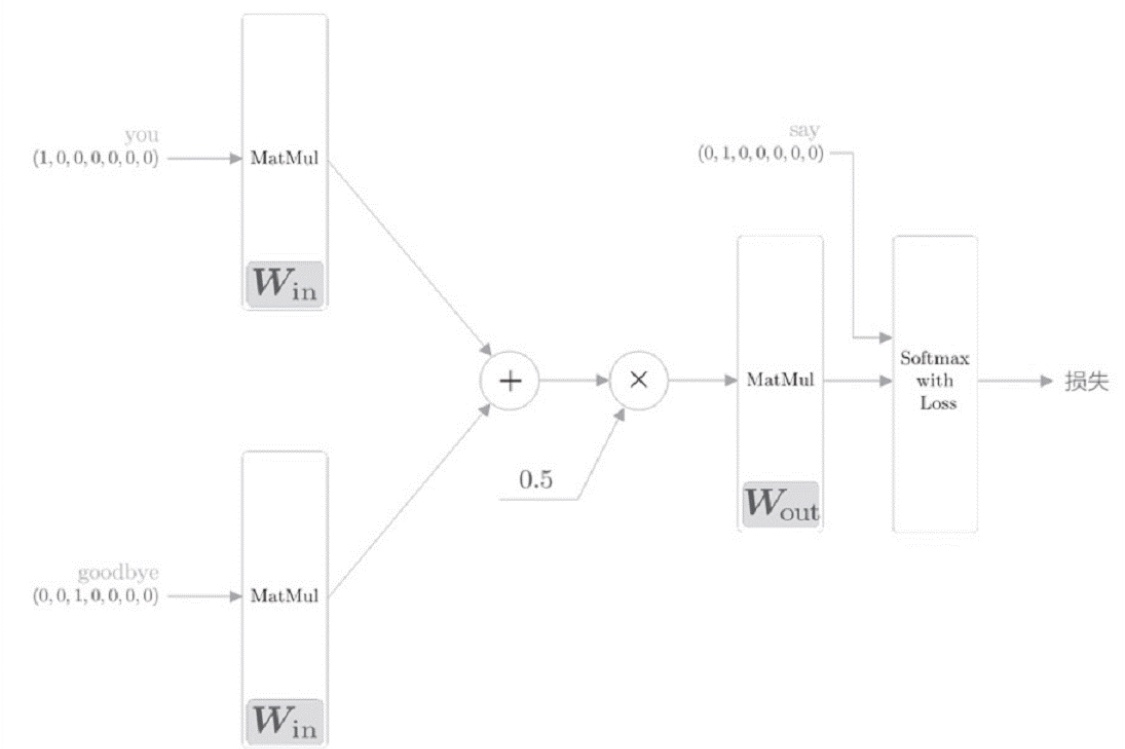
CBOW模型只是学习语料库中单词出现模式,如果语料库不一样,学习到的单词分布式表示也不一样。下面,我们为模型添加Softmax函数和交叉熵误差,利用这些概率和监督标签之间的交叉熵误差作为损失进行学习,如下图:
2.3 Word2vec的权重和分布式表示
word2vec中使用的网络有两个权重:输入侧的全连接的权重(每一行)、输出侧的全连接的权重(每一列),如下图:
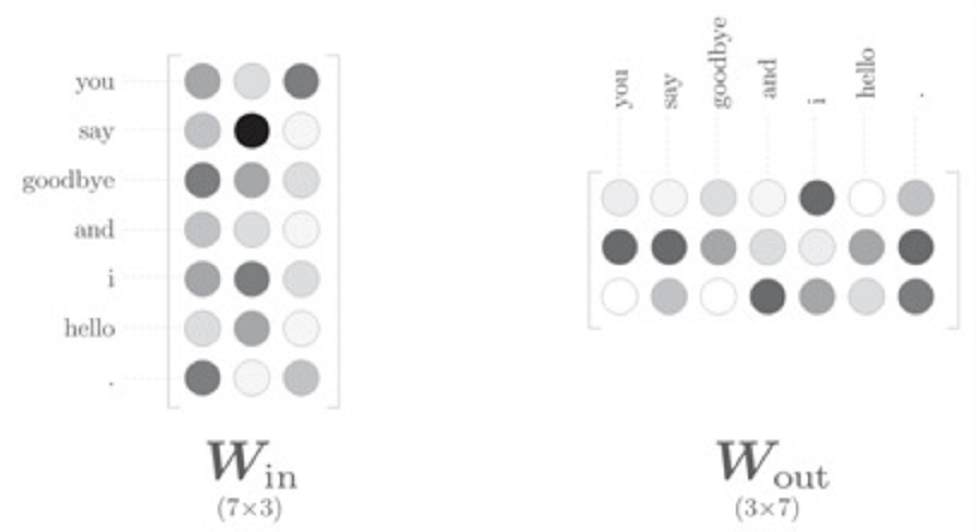
但是,我们到底应用哪个权重作为最终单词的分布式表是呢?常见的作法有3种:
- 只使用输入侧权重
- 只使用输出侧权重
- 同时使用(例:两者相加)
3.准备数据
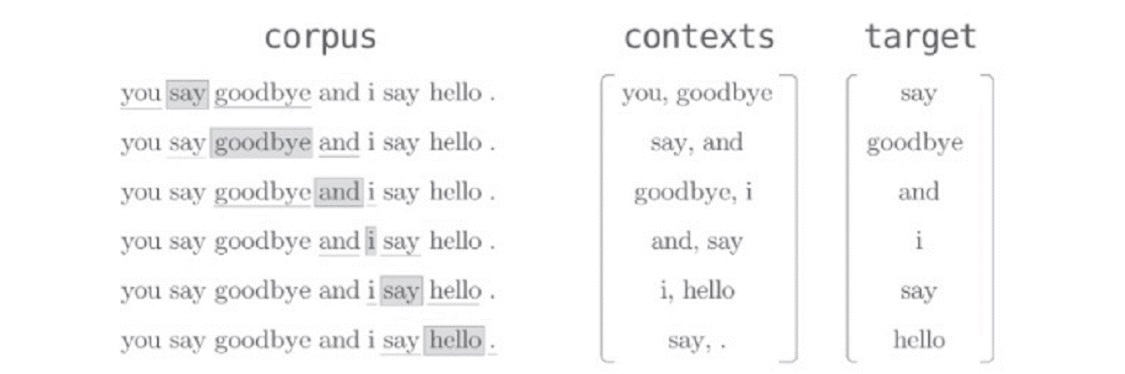
假设语料库中仅包含1句话“You say goodbye and I say hello”,上下文各取1个单词,可见下图上下文和所对应的标签:
下图为我们准备过程中的工作流程:

具体的代码实现如下:
def create_contexts_target(corpus, window_size=1):
'''生成上下文和目标词
:param corpus: 语料库(单词ID列表)
:param window_size: 窗口大小(当窗口大小为1时,左右各1个单词为上下文)
:return:
'''
target = corpus[window_size:-window_size]
contexts = []
for idx in range(window_size, len(corpus)-window_size):
cs = []
for t in range(-window_size, window_size + 1):
if t == 0:
continue
cs.append(corpus[idx + t])
contexts.append(cs)
return np.array(contexts), np.array(target)
def convert_one_hot(corpus, vocab_size):
'''转换为one-hot表示
:param corpus: 单词ID列表(一维或二维的NumPy数组)
:param vocab_size: 词汇个数
:return: one-hot表示(二维或三维的NumPy数组)
'''
N = corpus.shape[0]
if corpus.ndim == 1:
one_hot = np.zeros((N, vocab_size), dtype=np.int32)
for idx, word_id in enumerate(corpus):
one_hot[idx, word_id] = 1
elif corpus.ndim == 2:
C = corpus.shape[1]
one_hot = np.zeros((N, C, vocab_size), dtype=np.int32)
for idx_0, word_ids in enumerate(corpus):
for idx_1, word_id in enumerate(word_ids):
one_hot[idx_0, idx_1, word_id] = 1
return one_hot
利用上面的函数进行测试,查看对应的输出是否正确:
text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
vocab_size = len(word_to_id)
contexts, target = create_contexts_target(corpus, 1)
print(contexts)
print(target)
target = convert_one_hot(target, vocab_size)
print(target)
contexts = convert_one_hot(contexts, vocab_size)
print(contexts)
[[0 2]
[1 3]
[2 4]
[3 1]
[4 5]
[1 6]]
[1 2 3 4 1 5]
[[[1 0 0 0 0 0 0]
[0 0 1 0 0 0 0]]
[[0 1 0 0 0 0 0]
[0 0 0 1 0 0 0]]
[[0 0 1 0 0 0 0]
[0 0 0 0 1 0 0]]
[[0 0 0 1 0 0 0]
[0 1 0 0 0 0 0]]
[[0 0 0 0 1 0 0]
[0 0 0 0 0 1 0]]
[[0 1 0 0 0 0 0]
[0 0 0 0 0 0 1]]]
[[0 1 0 0 0 0 0]
[0 0 1 0 0 0 0]
[0 0 0 1 0 0 0]
[0 0 0 0 1 0 0]
[0 1 0 0 0 0 0]
[0 0 0 0 0 1 0]]
4.CBOW模型的构建与训练
4.1 CBOW模型的构建
首先,先创建SoftmaxWithLoss层:
class SoftmaxWithLoss:
def __init__(self):
self.params, self.grads = [], []
self.y = None # softmax的输出
self.t = None # 监督标签
def forward(self, x, t):
self.t = t
self.y = softmax(x)
# 在监督标签为one-hot向量的情况下,转换为正确解标签的索引
if self.t.size == self.y.size:
self.t = self.t.argmax(axis=1)
loss = cross_entropy_error(self.y, self.t)
return loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
dx = self.y.copy()
dx[np.arange(batch_size), self.t] -= 1
dx *= dout
dx = dx / batch_size
return dx
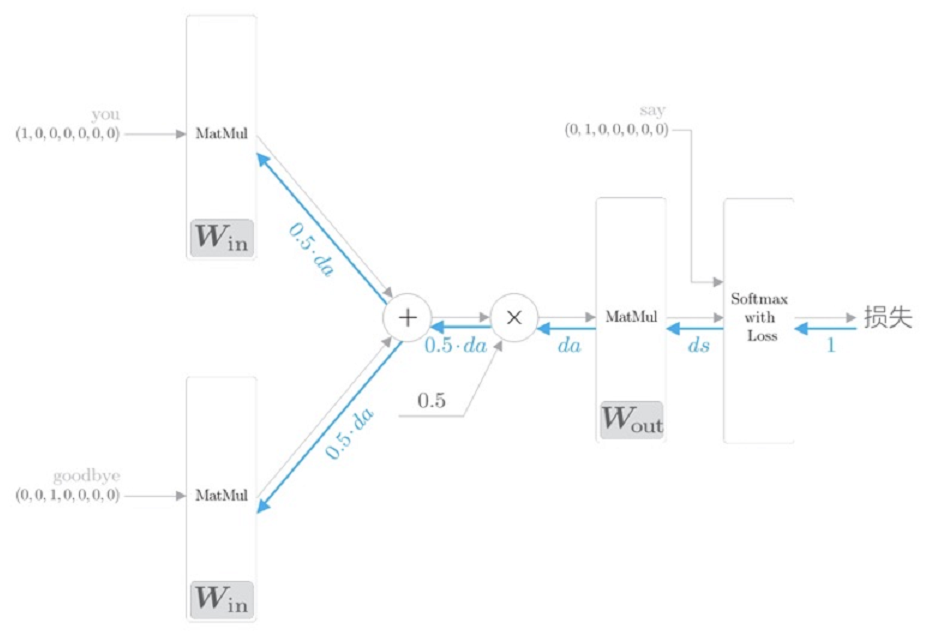
然后,再创建网络模型:
class SimpleCBOW:
def __init__(self, vocab_size, hidden_size):
V, H = vocab_size, hidden_size
# 初始化权重
W_in = 0.01 * np.random.randn(V, H).astype('f')
W_out = 0.01 * np.random.randn(H, V).astype('f')
# 生成层
self.in_layer0 = MatMul(W_in)
self.in_layer1 = MatMul(W_in)
self.out_layer = MatMul(W_out)
self.loss_layer = SoftmaxWithLoss()
# 将所有的权重和梯度整理到列表中
layers = [self.in_layer0, self.in_layer1, self.out_layer]
self.params, self.grads = [], []
for layer in layers:
self.params += layer.params
self.grads += layer.grads
# 将单词的分布式表示设置为成员变量
self.word_vecs = W_in
def forward(self, contexts, target):
h0 = self.in_layer0.forward(contexts[:, 0])
h1 = self.in_layer1.forward(contexts[:, 1])
h = (h0 + h1) * 0.5
score = self.out_layer.forward(h)
loss = self.loss_layer.forward(score, target)
return loss
def backward(self, dout=1):
ds = self.loss_layer.backward(dout)
da = self.out_layer.backward(ds)
da *= 0.5
self.in_layer1.backward(da)
self.in_layer0.backward(da)
return None
4.2 CBOW模型的训练
# ===========参数初始化===========
window_size = 1
hidden_size = 5
batch_size = 3
max_epoch = 1000
# ===========数据获取===========
text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
vocab_size = len(word_to_id)
contexts, target = create_contexts_target(corpus, window_size)
target = convert_one_hot(target, vocab_size)
contexts = convert_one_hot(contexts, vocab_size)
# ===========模型创建===========
model = SimpleCBOW(vocab_size, hidden_size)
optimizer = Adam()
trainer = Trainer(model, optimizer)
# ===========模型训练===========
trainer.fit(contexts, target, max_epoch, batch_size)
# ===========绘制图像===========
trainer.plot()
# ===========查看单词的分布式表示===========
word_vecs = model.word_vecs
for word_id, word in id_to_word.items():
print(word, word_vecs[word_id])
| epoch 1 | iter 1 / 2 | time 0[s] | loss 1.95
| epoch 2 | iter 1 / 2 | time 0[s] | loss 1.95
| epoch 3 | iter 1 / 2 | time 0[s] | loss 1.95
| epoch 4 | iter 1 / 2 | time 0[s] | loss 1.95
| epoch 5 | iter 1 / 2 | time 0[s] | loss 1.95
.................................................
| epoch 995 | iter 1 / 2 | time 0[s] | loss 0.56
| epoch 996 | iter 1 / 2 | time 0[s] | loss 0.44
| epoch 997 | iter 1 / 2 | time 0[s] | loss 0.75
| epoch 998 | iter 1 / 2 | time 0[s] | loss 0.37
| epoch 999 | iter 1 / 2 | time 0[s] | loss 0.49
| epoch 1000 | iter 1 / 2 | time 0[s] | loss 0.56
you [ 1.1102228 1.0799185 1.1570032 1.3092333 -1.0797074]
say [-1.2390769 -1.2460105 -0.33962205 -0.01357299 1.2468936 ]
goodbye [ 0.8573794 0.8571078 0.72916013 0.5650708 -0.89292306]
and [-1.0596409 -1.0813452 -1.5950402 -1.6030823 1.0973382]
i [ 0.8437616 0.8604424 0.7089162 0.5558257 -0.9147933]
hello [ 1.115681 1.0917497 1.1717849 1.3301636 -1.0921656]
. [-1.0579013 -1.0778097 1.4633303 1.3878536 0.9920829]

到此为止,我们已经将单词表示为密集向量,这就是基于推理方法的分布式表示,这样的表示能更好的捕捉单词的含义,但是由于我们实验的语料库十分小,在实际应用时,效果并不会太好,这些在面对庞大的语料库的时候便会迎刃而解,但是又不得不面对处理速度的问题(之后会改进)。
5.Word2vec背后的概率原理
5.1 CBOW模型
如下图所示,CBOW模型是根据上下文来推理中间词,因此我们可以将其看作是条件概率:
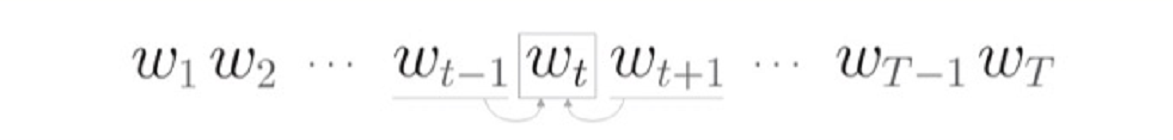
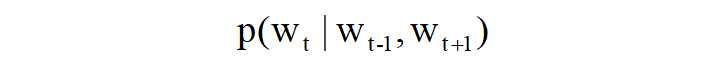
我们之前的网络模型是利用交叉熵误差函数,其表达式如下图:
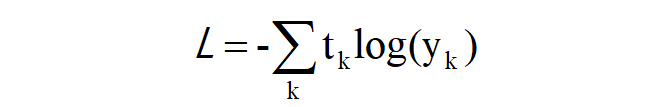
式子中的y(k)表示第k个事件发生的概率,t(k)表示监督标签采用one-hot编码,因此我们便可以将上面的概率表达式代入到交叉熵误差函数中,化简后便可以得到下面的表达式(负对数似然):
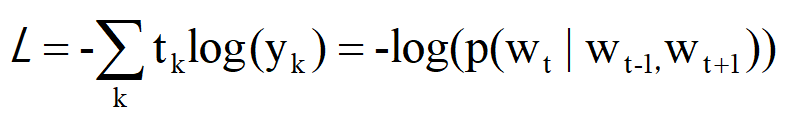
最后,我们再将一份样本数据扩展到整个语料库,则能得出最终的损失函数:
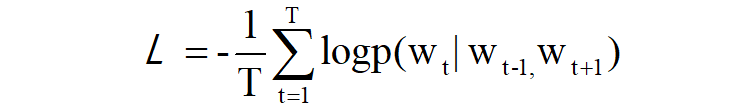
CBOW模型训练的任务就是让损失函数的值尽可能的小,此时的网络权重便是我们想要的单词分布式表示。
5.2 Skip-gram模型
如下图所示,Skip-gram模型是根据中间词来推理上下文,其对应的网络结构也如下图:

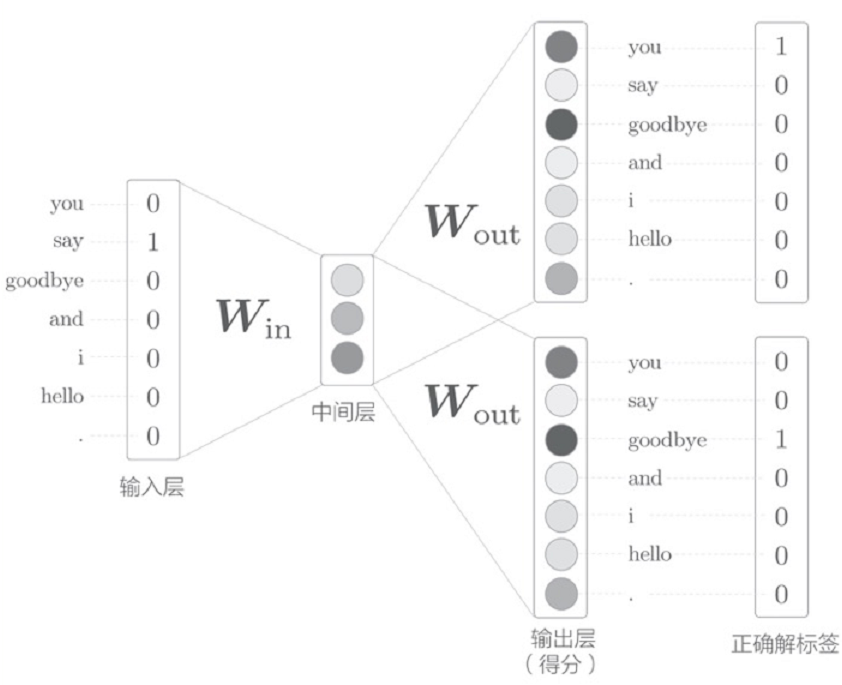
Skip-gram模型的输入层只有一个,输出层的数量则与上下文的单词个数相等。因此,首先要分别求出各个输出层的损失,然后将它们加起来作为最后的损失。同样,我们仍然可以利用条件概率来表示,在w(t)发生的情况下,w(t-1)与w(t+1)同时发生的概率(假设:上下文的单词之间没有相关性“条件独立”),则其表达式可以写成如下这样:

再将其代入损失函数,并将其扩展到整个语料库,可以得到以下表达式:
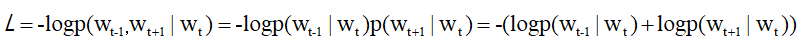
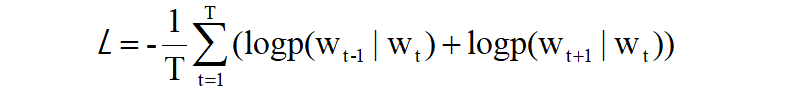
5.3 CBOW与Skip-gram对比
对于两种常见的模型,我们选择哪一种比较好?确切的说是选择“Skip-gram”。因为,从单词的分布式表示的精确度来看,在大多数情况下是Skip-gram模型表现的好,特别是随着语料库的增大,对于那些低频词和类推问题。但是,在性能提升的同时也伴随着资源消耗的增大,计算成本变大。
参考书籍与资料
《深度学习进阶---自然语言处理》:[日]斋藤康毅
《深度学习》:[美]伊恩古德费洛



评论